

Next: The moment generating function
Up: CVonline_moments
Previous: CVonline_moments
Moments are applicable to many different aspects of image processing, ranging from invariant pattern recognition and image encoding to pose estimation. When applied to images, they describe the image content (or distribution) with respect to its axes. They are designed
to capture both global and detailed geometric information about the image. Here we are using them to characterise a grey level image
so as to extract properties that have analogies in statistics or mechanics.
In continuous form an image can be considered as a two-dimensional Cartesian density distribution function 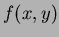
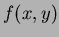 Two dimensional continuous function.
With this assumption, the general form of a moment of order
Two dimensional continuous function.
With this assumption, the general form of a moment of order 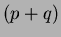 , evaluating over the complete image plane
, evaluating over the complete image plane 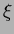 is:
is:
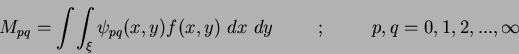 |
(1) |
The weighting kernel or basis function is  . This produces a weighted description of
. This produces a weighted description of 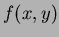 over the entire plane
over the entire plane 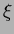 .
The basis functions may have a range of useful properties that may be passed onto the moments, producing descriptions which can be invariant under rotation, scale, translation and orientation.
To apply this to digital images, Equation 1.1 needs to be expressed in discrete form.
The probability density function (of a continuous distribution) is different from that of the probability of a discrete distribution.
For simplicity we assume that
.
The basis functions may have a range of useful properties that may be passed onto the moments, producing descriptions which can be invariant under rotation, scale, translation and orientation.
To apply this to digital images, Equation 1.1 needs to be expressed in discrete form.
The probability density function (of a continuous distribution) is different from that of the probability of a discrete distribution.
For simplicity we assume that 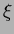 is divided into square pixels of dimensions
is divided into square pixels of dimensions 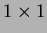 , with constant intensity
, with constant intensity 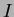 over each square pixel. So if
over each square pixel. So if 
 Discrete pixelis a discrete pixel value then:
Discrete pixelis a discrete pixel value then:
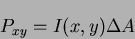 |
(2) |
where 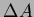 is the sample or pixel area equal to one.
Thus, analysing over the complete discrete image intensity plane produces:
is the sample or pixel area equal to one.
Thus, analysing over the complete discrete image intensity plane produces:
 |
(3) |
The choice of basis function depends on the application and any desired invariant properties. The choice of basis may introduce constraints including limiting the  and
and 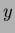 range, or translating the description and image to polar co-ordinates (eg. mapping it to the unit disc).
range, or translating the description and image to polar co-ordinates (eg. mapping it to the unit disc).
Subsections


Next: The moment generating function
Up: CVonline_moments
Previous: CVonline_moments
Jamie Shutler
2002-08-15
![]()
![]() Two dimensional continuous function.
With this assumption, the general form of a moment of order
Two dimensional continuous function.
With this assumption, the general form of a moment of order ![]() , evaluating over the complete image plane
, evaluating over the complete image plane ![]() is:
is:
